If Given Radians How Can You Tell What Quadrant It Is in

Radians

Radians are another fashion of measuring angles, and the mensurate of an bending can be converted betwixt degrees and radians.

Learning Objectives

Explain the definition of radians in terms of arc length of a unit circumvolve and use this to convert between degrees and radians

Central Takeaways

Key Points

• One radian is the measure of the central bending of a circumvolve such that the length of the arc is equal to the radius
  of the circle.
• A full revolution of a circumvolve ([latex]360^{\circ}[/latex]) equals [latex]2\pi~\mathrm{radians}[/latex]. This ways that [latex]\displaystyle{ 1\text{ radian} = \frac{180^{\circ}}{\pi} }[/latex]. [latex][/latex]
• The formula used to catechumen between radians and degrees is [latex]\displaystyle{ \text{angle in degrees} = \text{bending in radians} \cdot \frac{180^\circ}{\pi} }[/latex].
• The radian measure out of an angle is the ratio of the length of the arc to the radius of the circle [latex]\displaystyle{ \left(\theta = \frac{due south}{r}\correct) }[/latex]. In other words, if [latex]due south[/latex] is the length of an arc of a circumvolve, and [latex]r[/latex] is the radius of the circumvolve, then the central angle containing that arc measures radians.

Fundamental Terms

• arc: A continuous role of the circumference of a circle.
• circumference: The length of a line that bounds a circle.
• radian: The standard unit used to measure angles in mathematics. The measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circumvolve.

Introduction to Radians

Call up that dividing a circumvolve into 360 parts creates the degree measurement. This is an arbitrary measurement, and we may choose other ways to divide a circle. To find some other unit, think of the procedure of cartoon a circle. Imagine that you stop before the circle is completed. The portion that you drew is referred to as an arc. An arc may be a portion of a full circumvolve, a full circle, or more than a total circle, represented past more than one total rotation. The length of the arc around an entire circle is called the circumference of that circumvolve.

The circumference of a circle is

[latex]C = 2 \pi r[/latex]

If we divide both sides of this equation past [latex]r[/latex], we create the ratio of the circumference, which is always [latex]two\pi[/latex] to the radius, regardless of the length of the radius. So the circumference of any circle is [latex]2\pi \approx half dozen.28[/latex] times the length of the radius. That ways that if we took a string every bit long as the radius and used information technology to measure consecutive lengths around the circumference, at that place would be room for six full string-lengths and a fiddling more than a quarter of a seventh, equally shown in the diagram below.

The circumference of a circle compared to the radius: The circumference of a circumvolve is a little more than 6 times the length of the radius.

This brings usa to our new angle mensurate. The radian is the standard unit used to measure angles in mathematics. 1 radian is the measure out of a central bending of a circle that intercepts an arc equal in length to the radius of that circumvolve.

One radian: The bending [latex]t[/latex] sweeps out a measure of one radian. Note that the length of the intercepted arc is the same as the length of the radius of the circle.

Because the full circumference of a circle equals [latex]2\pi[/latex] times the radius, a full circular rotation is [latex]2\pi[/latex] radians.

Radians in a circle: An arc of a circle with the same length as the radius of that circle corresponds to an angle of 1 radian. A full circumvolve corresponds to an angle of [latex]2\pi[/latex] radians; this means that[latex]2\pi[/latex] radians is the same equally [latex]360^\circ[/latex].

Notation that when an angle is described without a specific unit, it refers to radian measure. For example, an angle measure of 3 indicates iii radians. In fact, radian measure out is dimensionless, since information technology is the quotient of a length (circumference) divided by a length (radius), and the length units cancel. You may sometimes run into radians represented by the symbol [latex]\text{rad}[/latex].

Comparing Radians to Degrees

Since we now know that the total range of a circle tin can exist represented by either 360 degrees or [latex]2\pi[/latex] radians, we can conclude the following:

[latex]\displaystyle{ \begin{align} 2\pi \text{ radians} &= 360^{\circ} \\ one\text{ radian} &= \frac{360^{\circ}}{2\pi} \\ i\text{ radian} &= \frac{180^{\circ}}{\pi} \finish{align}}[/latex]

As stated, one radian is equal to [latex]\displaystyle{ \frac{180^{\circ}}{\pi} }[/latex] degrees, or only under 57.3 degrees ([latex]57.3^{\circ}[/latex]). Thus, to convert from radians to degrees, we tin multiply by [latex]\displaystyle{ \frac{180^\circ}{\pi} }[/latex]:

[latex]\displaystyle{ \text{bending in degrees} = \text{angle in radians} \cdot \frac{180^\circ}{\pi} }[/latex]

A unit of measurement circle is a circle with a radius of 1, and it is used to prove certain common angles.

Unit of measurement circumvolve: Commonly encountered angles measured in radians and degrees.

Example

Convert an angle measuring [latex]\displaystyle{ \frac{\pi}{9} }[/latex] radians to degrees.

Substitute the angle in radians into the above formula:

[latex]\displaystyle{ \begin{marshal} \text{angle in degrees} &= \text{angle in radians} \cdot \frac{180^\circ}{\pi} \\ \text{bending in degrees} &= \frac{\pi}{9} \cdot \frac{180^\circ}{\pi} \\ &=\frac{180^{\circ}}{ix} \\ &= 20^{\circ} \stop{align} }[/latex]

Thus we accept [latex]\displaystyle{ \frac{\pi}{9} \text{ radians} = 20^{\circ} }[/latex].

Measuring an Angle in Radians

An arc length [latex]s[/latex] is the length of the curve along the arc. Just as the full circumference of a circle always has a constant ratio to the radius, the arc length produced by any given angle also has a constant relation to the radius, regardless of the length of the radius.

This ratio, chosen the radian mensurate, is the aforementioned regardless of the radius of the circle—it depends only on the angle. This property allows united states to define a measure of any angle as the ratio of the arc length [latex]s[/latex] to the radius [latex]r[/latex].

[latex]\displaystyle{ \begin{align} s &= r \theta \\ \theta &= \frac{southward}{r} \end{align} }[/latex]

Measuring radians: (a) In an bending of 1 radian; the arc lengths equals the radius [latex]r[/latex]. (b) An angle of 2 radians has an arc length [latex]s=2r[/latex]. (c) A full revolution is [latex]2\pi[/latex], or about 6.28 radians.

Instance

What is the measure of a given angle in radians if its arc length is [latex]4 \pi[/latex], and the radius has length [latex][/latex]12?

Substitute the values [latex]s = 4\pi[/latex] and [latex]r = 12[/latex] into the angle formula:

[latex]\displaystyle{ \begin{align} \theta &= \frac{s}{r} \\ & = \frac{4\pi}{12} \\ &= \frac{\pi}{3} \\ &= \frac{1}{iii}\pi \end{align} }[/latex]

The angle has a measure of [latex]\displaystyle{\frac{i}{three}\pi}[/latex] radians.

Defining Trigonometric Functions on the Unit Circle

Identifying points on a unit of measurement circle allows one to apply trigonometric functions to any angle.

Learning Objectives

Apply right triangles fatigued in the unit of measurement circle to ascertain the trigonometric functions for whatsoever angle

Key Takeaways

Central Points

• The [latex]10[/latex]– and [latex]y[/latex]-coordinates at a point on the unit circle given by an angle [latex]t[/latex] are defined past the functions [latex]x = \cos t[/latex] and [latex]y = \sin t[/latex].
• Although the tangent function is not indicated past the unit circumvolve, we can utilise the formula [latex]\displaystyle{\tan t = \frac{\sin t}{\cos t}}[/latex] to discover the tangent of whatever angle identified.
• Using the unit of measurement circle, we are able to employ trigonometric functions to any bending, including those greater than [latex]90^{\circ}[/latex].
• The unit circle demonstrates the periodicity of trigonometric functions by showing that they result in a repeated gear up of values at regular intervals.

Key Terms

• periodicity: The quality of a function with a repeated set of values at regular intervals.
• unit circle: A circumvolve centered at the origin with radius 1.
• quadrants: The four quarters of a coordinate plane, formed by the [latex]x[/latex]– and [latex]y[/latex]-axes.

Trigonometric Functions and the Unit of measurement Circumvolve

We have already divers the trigonometric functions in terms of right triangles. In this section, nosotros will redefine them in terms of the unit circle. Recall that a unit circumvolve is a circle centered at the origin with radius one. The angle [latex]t[/latex] (in radians ) forms an arc of length [latex]s[/latex].

The 10- and y-axes divide the coordinate plane (and the unit circle, since it is centered at the origin) into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, Ii, III, and Iv.

For any angle [latex]t[/latex], we can label the intersection of its side and the unit circumvolve past its coordinates, [latex](x, y)[/latex]. The coordinates [latex]x[/latex] and [latex]y[/latex] will be the outputs of the trigonometric functions [latex]f(t) = \cos t[/latex] and [latex]f(t) = \sin t[/latex], respectively. This means:

[latex]\displaystyle{ \brainstorm{align} x &= \cos t \\ ​y &= \sin t \end{align} }[/latex]

The diagram of the unit circle illustrates these coordinates.

Unit circle: Coordinates of a point on a unit of measurement circle where the cardinal angle is [latex]t[/latex] radians.

Note that the values of [latex]ten[/latex] and [latex]y[/latex] are given past the lengths of the two triangle legs that are colored red. This is a right triangle, and you tin can see how the lengths of these two sides (and the values of [latex]10[/latex] and [latex]y[/latex]) are given past trigonometric functions of [latex]t[/latex].

For an example of how this applies, consider the diagram showing the betoken with coordinates [latex]\displaystyle{\left(-\frac{\sqrt2}{2}, \frac{\sqrt2}{2}\right) }[/latex] on a unit circle.

Betoken on a unit circle: The point [latex]\displaystyle{ \left(-\frac{\sqrt2}{ii}, \frac{\sqrt2}{2}\right) }[/latex] on a unit circumvolve.

We know that, for any point on a unit circle, the [latex]x[/latex]-coordinate is [latex]\cos t[/latex] and the [latex]y[/latex]-coordinate is [latex]\sin t[/latex]. Applying this, nosotros can identify that [latex]\displaystyle{\cos t = -\frac{\sqrt2}{2}}[/latex] and  [latex]\displaystyle{\sin t = -\frac{\sqrt2}{two}}[/latex] for the angle [latex]t[/latex] in the diagram.

Recall that [latex]\displaystyle{\tan t = \frac{\sin t}{\cos t}}[/latex].  Applying this formula, nosotros can find the tangent of any angle identified by a unit circle as well. For the angle [latex]t[/latex] identified in the diagram  of the unit of measurement circle showing the point [latex]\displaystyle{\left(-\frac{\sqrt2}{2}, \frac{\sqrt2}{2}\correct)}[/latex], the tangent is:

[latex]\displaystyle{\begin{align}\tan t &= \frac{\sin t}{\cos t} \\&= \frac{-\frac{\sqrt2}{2}}{-\frac{\sqrt2}{2}} \\&= 1\end{marshal}}[/latex]

We take previously discussed trigonometric functions as they employ to correct triangles. This allowed usa to make observations virtually the angles and sides of right triangles, but these observations were limited to angles with measures less than [latex]xc^{\circ}[/latex]. Using the unit circumvolve, we are able to employ trigonometric functions to angles greater than [latex]xc^{\circ}[/latex].

Further Consideration of the Unit Circle

The coordinates of sure points on the unit circle and the the measure of each bending in radians and degrees are shown in the unit circumvolve coordinates diagram. This diagram allows one to make observations about each of these angles using trigonometric functions.

Unit of measurement circle coordinates: The unit circle, showing coordinates and bending measures of certain points.

Nosotros can find the coordinates of any point on the unit circle. Given whatever angle [latex]t[/latex], nosotros tin find the [latex]x[/latex]– or [latex]y[/latex]-coordinate at that point using [latex]10 = \text{cos } t[/latex]  and [latex]y = \text{sin } t[/latex].

The unit of measurement circle demonstrates the periodicity of trigonometric functions. Periodicity refers to the fashion trigonometric functions issue in a repeated set up of values at regular intervals. Take a wait at the [latex]10[/latex]-values of the coordinates in the unit circle above for values of [latex]t[/latex] from [latex]0[/latex] to [latex]two{\pi}[/latex]:

[latex]{1, \frac{\sqrt{3}}{two}, \frac{\sqrt{2}}{ii}, \frac{1}{2}, 0, -\frac{1}{two}, -\frac{\sqrt{2}}{2}, -\frac{\sqrt{3}}{2}, -ane, -\frac{\sqrt{3}}{ii}, -\frac{\sqrt{2}}{2}, -\frac{one}{2}, 0, \frac{one}{two}, \frac{\sqrt{two}}{2}, \frac{\sqrt{3}}{ii}, 1}[/latex]

We can identify a pattern in these numbers, which fluctuate between [latex]-1[/latex] and [latex]i[/latex]. Note that this pattern will repeat for higher values of [latex]t[/latex]. Call back that these [latex]ten[/latex]-values correspond to [latex]\cos t[/latex]. This is an indication of the periodicity of the cosine function.

Example

Solve [latex]\displaystyle{ \sin{ \left(\frac{seven\pi}{half dozen}\right) } }[/latex].

It seems similar this would exist complicated to work out. However, notice that the unit circle diagram shows the coordinates at [latex]\displaystyle{ t = \frac{7\pi}{6} }[/latex]. Since the [latex]y[/latex]-coordinate corresponds to [latex]\sin t[/latex], nosotros can identify that

[latex]\displaystyle{\sin{ \left(\frac{7\pi}{6}\correct)} = -\frac{1}{2} }[/latex]

Special Angles

The unit circle and a set of rules tin can be used to recollect the values of trigonometric functions of special angles.

Learning Objectives

Explain how the properties of sine, cosine, and tangent and their signs in each quadrant give their values for each of the special angles

Key Takeaways

Key Points

• The trigonometric functions for the angles in the unit circle tin exist memorized and recalled using a ready of rules.
• The sign on a trigonometric part depends on the quadrant that the angle falls in, and the mnemonic phrase "A Smart Trig Class" is used to identify which functions are positive in which quadrant.
• Reference angles in quadrant Iare used to identify which value any angle in quadrants Ii, 3, or IV will have. A reference bending forms the aforementioned angle with the [latex]x[/latex]-centrality as the angle in question.
• Only the sine and cosine functions for special angles are included in the unit circle. Still, since tangent is derived from sine and cosine, information technology can be calculated for any of the special angles.

Key Terms

• special angle: An angle that is a multiple of 30 or 45 degrees; trigonometric functions are hands written at these angles.

Trigonometric Functions of Special Angles

Remember that certain angles and their coordinates, which correspond to [latex]x = \cos t[/latex] and [latex]y = \sin t[/latex] for a given angle [latex]t[/latex], can exist identified on the unit circle.

Unit circumvolve: Special angles and their coordinates are identified on the unit of measurement circle.

The angles identified on the unit circumvolve higher up are chosen special angles; multiples of [latex]\pi[/latex], [latex]\frac{\pi}{2}[/latex], [latex][/latex][latex]\frac{\pi}{three}[/latex], [latex]\frac{\pi}{four}[/latex], and [latex]\frac{\pi}{6}[/latex] ([latex]180^\circ[/latex][latex][/latex], [latex]90^\circ[/latex], [latex]60^\circ[/latex],  [latex]45^\circ[/latex], and [latex]30^\circ[/latex]). These have relatively simple expressions. Such uncomplicated expressions generally do not exist for other angles. Some examples of the algebraic expressions for the sines of special angles are:

[latex]\displaystyle{ \begin{align} \sin{\left( 0^{\circ} \correct)} &= 0 \\ \sin{\left( xxx^{\circ} \correct)} &= \frac{i}{2} \\ \sin{\left( 45^{\circ} \right)} &= \frac{\sqrt{two}}{two} \\ \sin{\left( 60^{\circ} \right)} &= \frac{\sqrt{three}}{two} \\ \sin{\left( 90^{\circ} \right)} &= ane \\ \cease{marshal} }[/latex]

The expressions for the cosine functions of these special angles are besides simple.

Note that while only sine and cosine are divers directly past the unit circle, tangent tin can be defined every bit a quotient involving these two:

[latex]\displaystyle{ \tan t = \frac{\sin t}{\cos t} }[/latex]

Tangent functions as well have simple expressions for each of the special angles.

Nosotros tin observe this trend through an example. Permit'due south find the tangent of [latex]sixty^{\circ}[/latex].

First, we tin can identify from the unit circle that:

[latex]\displaystyle{ \begin{align} \sin{ \left(60^{\circ}\right) } &= \frac{\sqrt{3}}{two} \\ \cos{ \left(60^{\circ}\right) } &= \frac{1}{2} \end{marshal} }[/latex]

Nosotros can easily calculate the tangent:

[latex]\displaystyle{ \brainstorm{align} \tan{\left(60^{\circ}\right)} &= \frac{\sin{\left(60^{\circ}\right)}}{\cos{\left(sixty^{\circ}\right)}} \\ &= \frac{\frac{\sqrt{iii}}{2}}{\frac{1}{2}} \\ &= \frac{\sqrt{3}}{two} \cdot \frac{ii}{1} \\ &= \sqrt{three} \end{marshal} }[/latex]

Memorizing Trigonometric Functions

An understanding of the unit circle and the ability to quickly solve trigonometric functions for sure angles is very useful in the field of mathematics. Applying rules and shortcuts associated with the unit circle allows y'all to solve trigonometric functions rapidly. The following are some rules to help you quickly solve such problems.

Signs of Trigonometric Functions

The sign of a trigonometric part depends on the quadrant that the angle falls in. To aid remember which of the trigonometric functions are positive in each quadrant, nosotros can employ the mnemonic phrase "A Smart Trig Form." Each of the iv words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is "A," all of the trigonometric functions are positive. In quadrant Two, "Smart," only sine is positive. In quadrant III, "Trig," only tangent is positive. Finally, in quadrant Four, "Class," only cosine is positive.

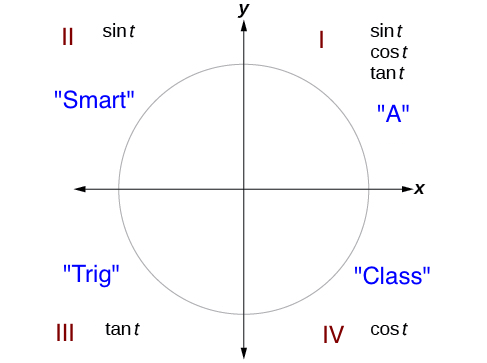
Sign rules for trigonometric functions: The trigonometric functions are each listed in the quadrants in which they are positive.

Identifying Values Using Reference Angles

Take a close look at the unit circle, and note that [latex]\sin t[/latex] and [latex]\cos t[/latex] take certain values every bit they fluctuate between [latex]-1[/latex] and [latex]1[/latex]. You will notice that they accept on the value of nix, also every bit the positive and negative values of three particular numbers: [latex]\displaystyle{\frac{\sqrt{iii}}{ii}}[/latex], [latex]\displaystyle{\frac{\sqrt{2}}{two}}[/latex], and [latex]\displaystyle{\frac{1}{2}}[/latex]. Identifying reference angles will help usa identify a pattern in these values.

Reference angles in quadrant I are used to identify which value any bending in quadrants Two, III, or Iv will take. This means that nosotros just need to memorize the sine and cosine of three angles in quadrant I: [latex]30^{\circ}[/latex], [latex]45^{\circ}[/latex], and [latex]60^{\circ}[/latex].

For any given angle in the get-go quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the [latex]y[/latex]-coordinate on the unit circle, the other angle with the same sine volition share the same [latex]y[/latex]-value, just accept the contrary [latex]ten[/latex]-value. Therefore, its cosine value will be the opposite of the showtime angle's cosine value.

Too, there will be an angle in the fourth quadrant with the same cosine as the original angle. The bending with the same cosine will share the aforementioned [latex]10[/latex]-value but will have the contrary [latex]y[/latex]-value. Therefore, its sine value will be the opposite of the original angle'south sine value.

As shown in the diagrams below, angle [latex]\blastoff[/latex] has the same sine value as angle [latex]t[/latex]; the cosine values are opposites. Angle [latex]\beta[/latex] has the aforementioned cosine value as bending [latex]t[/latex]; the sine values are opposites.

[latex]\displaystyle{ \begin{align} \sin t = \sin \alpha \quad &\text{and} \quad \cos t = -\cos \alpha \\ \sin t = -\sin \beta \quad &\text{and} \quad \cos t = \cos \beta \end{align} }[/latex]

Reference angles: In the left figure, [latex]t[/latex] is the reference angle for [latex]\blastoff[/latex]. In the right figure, [latex]t[/latex] is the reference bending for [latex]\beta[/latex].

Recall that an angle'due south reference bending is the acute angle, [latex]t[/latex], formed by the terminal side of the bending [latex]t[/latex] and the horizontal axis. A reference angle is always an angle between [latex]0[/latex] and [latex]90^{\circ}[/latex], or [latex]0[/latex] and [latex]\displaystyle{\frac{\pi}{2}}[/latex] radians. For any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

Reference angles in each quadrant: For any angle in quadrants Two, 3, or Four, there is a reference angle in quadrant I.

Thus, in social club to recall any sine or cosine of a special angle, you need to be able to identify its bending with the [latex]x[/latex]-axis in order to compare it to a reference angle. You lot volition and so place and apply the appropriate sign for that trigonometric function in that quadrant.

These are the steps for finding a reference angle for whatsoever angle between [latex]0[/latex] and [latex]2\pi[/latex]:

1. An angle in the first quadrant is its own reference angle.
2. For an angle in the second or third quadrant, the reference bending is [latex]|\pi - t|[/latex] or [latex]|180^{\circ} - t|[/latex].
3. For an angle in the fourth quadrant, the reference angle is [latex]2\pi - t[/latex] or [latex]360^{\circ} - t[/latex]. If an bending is less than [latex]0[/latex] or greater than [latex]2\pi[/latex], add or decrease [latex]2\pi[/latex] equally many times as needed to find an equivalent bending between [latex]0[/latex] and [latex]2\pi[/latex].

Since tangent functions are derived from sine and cosine, the tangent can exist calculated for any of the special angles by first finding the values for sine or cosine.

Example

Find [latex]\tan (225^{\circ})[/latex], applying the rules above.

First, note that [latex]225^{\circ}[/latex] falls in the third quadrant:

Angle [latex]225^{\circ}[/latex] on a unit circle: The angle [latex]225^{\circ}[/latex]falls in quadrant Iii.

Subtract [latex]225^{\circ}[/latex] from [latex]180^{\circ}[/latex] to identify the reference bending:

[latex]\displaystyle{ \begin{align} \left| 180^{\circ} - 225^{\circ} \right| &= \left|-45^{\circ} \right| \\ &= 45^{\circ} \terminate{align} }[/latex]

In other words, [latex]225^{\circ}[/latex] falls [latex]45^{\circ}[/latex] from the [latex]ten[/latex]-axis. The reference angle is [latex]45^{\circ}[/latex].

Recall that

[latex]\displaystyle{\sin{ \left(45^{\circ}\correct)} = \frac{\sqrt{2}}{two} }[/latex]

However, the rules described above tell us that the sine of an angle in the third quadrant is negative. So we have

[latex]\displaystyle{\sin{ \left(225^{\circ}\right)} = -\frac{\sqrt{2}}{2} }[/latex]

Following the aforementioned process for cosine, we can identify that

[latex]\displaystyle{ \cos{ \left(225^{\circ}\right)} = -\frac{\sqrt{2}}{2} }[/latex]

We can detect [latex]\tan (225^{\circ})[/latex] by dividing [latex]\sin (225^{\circ})[/latex] by [latex]\cos (225^{\circ})[/latex]:

[latex]\displaystyle{ \begin{align} \tan{ \left(225^{\circ}\right)} &= \frac{\sin(225^{\circ})}{\cos (225^{\circ})} \\ &= \frac{-\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}} \\ &= -\frac{\sqrt{two}}{2} \cdot -\frac{2}{\sqrt{2}} \\ &= 1 \cease{align} }[/latex]

Sine and Cosine every bit Functions

The functions sine and cosine tin can be graphed using values from the unit circle, and certain characteristics tin can be observed in both graphs.

Learning Objectives

Describe the characteristics of the graphs of sine and cosine

Key Takeaways

Primal Points

• Both the sine function [latex](y = \sin x)[/latex] and cosine role [latex](y = \cos x)[/latex] tin can be graphed by plotting points derived from the unit circle, with each [latex]x[/latex]-coordinate being an bending in radians and the [latex]y[/latex]-coordinate existence the corresponding value of the office at that bending.
• Sine and cosine are periodic functions with a period of [latex]2\pi[/latex].
• Both sine and cosine accept a domain of [latex](-\infty, \infty)[/latex] and a range of [latex][-1, one][/latex].
• The graph of [latex]y = \sin x[/latex] is symmetric well-nigh the origin because it is an odd function, while the graph of [latex]y = \cos x[/latex] is symmetric almost the [latex]y[/latex]-axis because information technology is an even function.

Central Terms

• period: An interval containing values that occur repeatedly in a part.
• even function: A continuous set of [latex]\left(x,f(x)\right)[/latex] points in which [latex]f(-x) = f(ten)[/latex], with symmetry most the [latex]y[/latex]-centrality.
• odd part: A continuous set of [latex]\left(x, f(10)\right)[/latex] points in which [latex]f(-x) = -f(x)[/latex], with symmetry about the origin.
• periodic function: A continuous set of [latex]\left(ten,f(x)\right)[/latex] points that repeats at regular intervals.

Graphing Sine and Cosine Functions

Recall that the sine and cosine functions chronicle real number values to the [latex]ten[/latex]– and [latex]y[/latex]-coordinates of a bespeak on the unit circumvolve. And so what do they look like on a graph on a coordinate plane? Permit'southward start with the sine role, [latex]y = \sin 10[/latex]. Nosotros tin can create a table of values and use them to sketch a graph. Below are some of the values for the sine function on a unit of measurement circle, with the [latex]x[/latex]-coordinate existence the bending in radians and the [latex]y[/latex]-coordinate being [latex]\sin x[/latex]:

[latex]\displaystyle{ (0, 0) \quad (\frac{\pi}{6}, \frac{one}{2}) \quad (\frac{\pi}{4}, \frac{\sqrt{ii}}{2}) \quad (\frac{\pi}{iii}, \frac{\sqrt{3}}{ii}) \quad (\frac{\pi}{two}, i) \\ (\frac{2\pi}{iii}, \frac{\sqrt{iii}}{2}) \quad (\frac{3\pi}{4}, \frac{\sqrt{2}}{2}) \quad (\frac{5\pi}{6}, \frac{1}{2}) \quad (\pi, 0) }[/latex]

Plotting the points from the table and continuing along the [latex]10[/latex]-centrality gives the shape of the sine part.

Graph of the sine function: Graph of points with [latex]x[/latex] coordinates being angles in radians, and [latex]y[/latex] coordinates beingness the function [latex]\sin x[/latex].

Notice how the sine values are positive between [latex]0[/latex] and [latex]\pi[/latex], which correspond to the values of the sine part in quadrants I and Two on the unit circumvolve, and the sine values are negative betwixt [latex]\pi[/latex] and [latex]2\pi[/latex], which represent to the values of the sine role in quadrants III and IV on the unit of measurement circumvolve.

Plotting values of the sine function: The points on the curve [latex]y = \sin x[/latex] correspond to the values of the sine role on the unit circle.

Now allow's have a like look at the cosine function, [latex]f(x) = \sin x[/latex]. Over again, we can create a table of values and use them to sketch a graph. Beneath are some of the values for the sine office on a unit circle, with the [latex]10[/latex]-coordinate existence the angle in radians and the [latex]y[/latex]-coordinate being [latex]\cos x[/latex]:

[latex]\displaystyle{ (0, i) \quad (\frac{\pi}{6}, \frac{\sqrt{iii}}{ii}) \quad (\frac{\pi}{4}, \frac{\sqrt{2}}{2}) \quad (\frac{\pi}{3}, \frac{1}{2}) \quad (\frac{\pi}{2}, 0) \\ (\frac{ii\pi}{3}, -\frac{one}{2}) \quad (\frac{3\pi}{iv}, -\frac{\sqrt{2}}{two}) \quad (\frac{5\pi}{6}, -\frac{\sqrt{3}}{2}) \quad (\pi, -1) }[/latex]

Every bit with the sine role, we can plots points to create a graph of the cosine role.

Graph of the cosine function: The points on the curve [latex]y = \cos x[/latex] correspond to the values of the cosine function on the unit circle.

Considering nosotros tin can evaluate the sine and cosine of any real number, both of these functions are defined for all real numbers. By thinking of the sine and cosine values every bit coordinates of points on a unit circle, information technology becomes articulate that the range of both functions must be the interval [latex]\left[-one, 1 \right][/latex].

Identifying Periodic Functions

In the graphs for both sine and cosine functions, the shape of the graph repeats after [latex]2\pi[/latex], which means the functions are periodic with a period of [latex]two\pi[/latex]. A periodic office is a function with a repeated ready of values at regular intervals. Specifically, it is a function for which a specific horizontal shift, [latex]P[/latex], results in a function equal to the original function:

[latex]f(x + P) = f(10)[/latex]

for all values of [latex]x[/latex] in the domain of [latex]f[/latex]. When this occurs, we call the smallest such horizontal shift with [latex]P>0[/latex] the period of the role. The diagram below shows several periods of the sine and cosine functions.

Periods of the sine and cosine functions: The sine and cosine functions are periodic, meaning that a specific horizontal shift, [latex]P[/latex], results in a function equal to the original function:[latex]f(x + P) = f(x)[/latex].

Even and Odd Functions

Looking once again at the sine and cosine functions on a domain centered at the [latex]y[/latex]-axis helps reveal symmetries. As nosotros tin can run across in the graph of the sine function, it is symmetric about the origin, which indicates that it is an odd function. All along the graph, any two points with opposite [latex]x[/latex] values also accept opposite [latex]y[/latex] values. This is feature of an odd office: two inputs that are opposites have outputs that are also opposites. In other words, if [latex]\sin (-10) = - \sin x[/latex].

Odd symmetry of the sine function: The sine function is odd, meaning information technology is symmetric virtually the origin.

The graph of the cosine function shows that it is symmetric nearly the y-axis. This indicates that it is an fifty-fifty function. For even functions, whatsoever two points with opposite [latex]x[/latex]-values have the same function value. In other words, [latex]\cos (-x) = \cos ten[/latex]. We can run into from the graph that this is true by comparison the [latex]y[/latex]-values of the graph at any opposite values of [latex]x[/latex].

Fifty-fifty symmetry of the cosine function: The cosine role is fifty-fifty, pregnant it is symmetric virtually the [latex]y[/latex]-axis.

Tangent equally a Function

Characteristics of the tangent function tin can be observed in its graph.

Learning Objectives

Draw the characteristics of the graph of the tangent function

Fundamental Takeaways

Cardinal Points

• The tangent function is undefined at any value of [latex]10[/latex] where [latex]\cos 10 = 0[/latex], and its graph has vertical asymptotes at these [latex]x[/latex] values.
• Tangent is a periodic function with a flow of [latex]\pi[/latex].
• The graph of the tangent office is symmetric around the origin, and thus is an odd office.

Key Terms

• periodic function: A continuous set of [latex]\left(x, f(ten)\right)[/latex] points with a set of values that repeats at regular intervals.
• menstruation: An interval containing the minimum ready of values that repeat in a periodic function.
• odd office: An continuous set up of [latex]\left(10, f(x)\right)[/latex] points in which [latex]f(-x) = -f(x)[/latex], and there is symmetry about the origin.
• vertical asymptote: A straight line parallel to the [latex]y[/latex] axis that a curve approaches arbitrarily closely as the curve goes to infinity.

Graphing the Tangent Function

The tangent part can exist graphed by plotting [latex]\left(x,f(x)\right)[/latex]  points. The shape of the part can be created by finding the values of the tangent at special angles. However, it is not possible to discover the tangent functions for these special angles with the unit circle. We apply the formula, [latex]\displaystyle{ \tan x = \frac{\sin x}{\cos x} }[/latex] to decide the tangent for each value.

Nosotros can analyze the graphical beliefs of the tangent function by looking at values for some of the special angles. Consider the points below, for which the [latex]x[/latex]-coordinates are angles in radians, and the [latex]y[/latex]-coordinates are [latex]\tan x[/latex]:

[latex]\displaystyle{ (-\frac{\pi}{2}, \text{undefined}) \quad (-\frac{\pi}{3}, -\sqrt{iii}) \quad (-\frac{\pi}{4}, -1) \quad (-\frac{\pi}{6}, -\frac{\sqrt{iii}}{3}) \quad (0, 0) \\ (\frac{\pi}{6}, \frac{\sqrt{3}}{three}) \quad (\frac{\pi}{4}, one) \quad (\frac{\pi}{3}, \sqrt{3}) \quad (\frac{\pi}{ii}, \text{undefined}) }[/latex]

Notice that [latex]\tan x[/latex] is undefined at [latex]\displaystyle{x = -\frac{\pi}{two}}[/latex] and [latex]\displaystyle{x = \frac{\pi}{2}}[/latex]. The in a higher place points volition help united states of america draw our graph, just we need to decide how the graph behaves where it is undefined. Let's consider the last four points. We can identify that the values of [latex]y[/latex] are increasing equally [latex]x[/latex] increases and approaches [latex]\displaystyle{\frac{\pi}{2}}[/latex]. We could consider additional points betwixt [latex]\displaystyle{ten=0}[/latex] and [latex]\displaystyle{10 = \frac{\pi}{ii}}[/latex], and nosotros would see that this holds. Also, nosotros can see that [latex]y[/latex] decreases equally [latex]x[/latex] approaches [latex]\displaystyle{-\frac{\pi}{2}}[/latex], because the outputs become smaller and smaller.

Recall that in that location are multiple values of [latex]10[/latex] that tin can requite [latex]\cos ten = 0[/latex]. At whatever such indicate, [latex]\tan x[/latex] is undefined because [latex]\displaystyle{\tan x = \frac{\sin x}{\cos x}}[/latex]. At values where the tangent office is undefined, there are discontinuities in its graph. At these values, the graph of the tangent has vertical asymptotes.

Graph of the tangent function: The tangent function has vertical asymptotes at [latex]\displaystyle{x = \frac{\pi}{2}}[/latex] and [latex]\displaystyle{x = -\frac{\pi}{two}}[/latex].

Characteristics of the Graph of the Tangent Function

Equally with the sine and cosine functions, tangent is a periodic office. This means that its values repeat at regular intervals. The period of the tangent function is [latex]\pi[/latex] considering the graph repeats itself on [latex]10[/latex]-centrality intervals of [latex]m\pi[/latex], where [latex]k[/latex] is a abiding. In the graph of the tangent function on the interval [latex]\displaystyle{-\frac{\pi}{2}}[/latex] to [latex]\displaystyle{\frac{\pi}{2}}[/latex], we tin can meet the behavior of the graph over ane consummate cycle of the role. If we wait at
any larger interval, we will run across that the characteristics of the graph echo.

The graph of the tangent function is symmetric around the origin, and thus is an odd part. In other words, [latex]\text{tan}(-10) = - \text{tan } x[/latex] for any value of [latex]ten[/latex]. Any two points with contrary values of [latex]x[/latex] produce reverse values of [latex]y[/latex]. We can run into that this is true by because the [latex]y[/latex] values of the graph at any opposite values of [latex]x[/latex]. Consider [latex]\displaystyle{x=\frac{\pi}{iii}}[/latex] and [latex]\displaystyle{x=-\frac{\pi}{three}}[/latex]. We already adamant above that [latex]\displaystyle{\tan (\frac{\pi}{iii}) = \sqrt{iii}}[/latex], and [latex]\displaystyle{\tan (-\frac{\pi}{three}) = -\sqrt{3}}[/latex].

Secant and the Trigonometric Cofunctions

Trigonometric functions take reciprocals that tin can be calculated using the unit circle.

Learning Objectives

Calculate values for the trigonometric functions that are the reciprocals of sine, cosine, and tangent

Central Takeaways

Central Points

• The secant function is the reciprocal of the cosine role [latex]\displaystyle{\left(\sec x = \frac{1}{\cos x}\right)}[/latex]. It can exist institute for an angle [latex]t[/latex] past using the [latex]x[/latex]-coordinate of  the associated point on the unit of measurement circumvolve: [latex]\displaystyle{\sec t = \frac{1}{ten}}[/latex].
• The cosecant function is the reciprocal of the sine role [latex]\displaystyle{\left(\csc x = \frac{ane}{\sin ten}\right)}[/latex]. Information technology tin can exist constitute for an angle [latex]t[/latex] by using the [latex]y[/latex]-coordinate of  the associated point on the unit of measurement circle: [latex]\displaystyle{\csc t = \frac{1}{y}}[/latex].
• The cotangent function is the reciprocal of the tangent function [latex]\displaystyle{\left(\cot x = \frac{1}{\tan x} = \frac{\cos t}{\sin t}\right)}[/latex]. It can exist found for an angle by using the [latex]ten[/latex]– and [latex]y[/latex]-coordinates of  the associated point on the unit circle: [latex]\displaystyle{\cot t = \frac{\cos t}{\sin t} = \frac{10}{y}}[/latex].

Key Terms

• secant: The reciprocal of the cosine function
• cosecant: The reciprocal of the sine function
• cotangent: The reciprocal of the tangent part

Introduction to Reciprocal Functions

We have discussed 3 trigonometric functions: sine, cosine, and tangent. Each of these functions has a reciprocal part, which is divers by the reciprocal of the ratio for the original trigonometric role. Note that reciprocal functions differ from inverse functions. Inverse functions are a fashion of working backwards, or determining an bending given a trigonometric ratio; they involve working with the same ratios every bit the original role.

The iii reciprocal functions are described below.

Secant

The secant part is the reciprocal of the cosine office, and is abbreviated as [latex]\sec[/latex].
It can be described as the ratio of the length of the hypotenuse to the length of the side by side side in a triangle.

[latex]\displaystyle{ \begin{align} \sec x &= \frac{1}{\cos ten} \\ \sec 10 &= \frac{\text{hypotenuse}}{\text{adjacent}} \end{align} }[/latex]

It is like shooting fish in a barrel to summate secant with values in the unit circumvolve. Remember that for any point on the circumvolve, the [latex]x[/latex]-value gives [latex]\cos t[/latex] for the associated angle [latex]t[/latex]. Therefore, the secant function for that angle is

[latex]\displaystyle{\sec t = \frac{i}{x}}[/latex]

Cosecant

The cosecant office is the reciprocal of the sine function, and is abbreviated as[latex]\csc[/latex]. It tin be described every bit the ratio of the length of the hypotenuse to the length of the opposite side in a triangle.

[latex]\displaystyle{ \begin{align} \csc 10 &= \frac{1}{\sin ten} \\ \csc x &= \frac{\text{hypotenuse}}{\text{contrary}} \end{marshal} }[/latex]

As with secant, cosecant can be calculated with values in the unit circle. Think that for any betoken on the circumvolve, the [latex]y[/latex]-value gives [latex]\sin t[/latex]. Therefore, the cosecant part for the same bending is

[latex]\displaystyle{\csc t = \frac{ane}{y}}[/latex]

Cotangent

The cotangent function is the reciprocal of the tangent function, and is abbreviated as [latex]\cot[/latex]. It can be described as the ratio of the length of the side by side side to the length of the hypotenuse in a triangle.

[latex]\displaystyle{ \begin{marshal} \cot x &= \frac{1}{\tan ten} \\ \cot ten &= \frac{\text{adjacent}}{\text{contrary}} \finish{align} }[/latex]

Besides note that because [latex]\displaystyle{\tan 10 = \frac{\sin x}{\cos x}}[/latex], its reciprocal is

[latex]\displaystyle{\cot x = \frac{\cos 10}{\sin 10}}[/latex]

Cotangent can as well be calculated with values in the unit of measurement circumvolve. Applying the [latex]x[/latex]– and [latex]y[/latex]-coordinates associated with bending [latex]t[/latex], we have

[latex]\displaystyle{ \begin{align} \cot t &= \frac{\cos t}{\sin t} \\ \cot t &= \frac{x}{y} \stop{align} }[/latex]

Calculating Reciprocal Functions

We now recognize six trigonometric functions that tin can be calculated using values in the unit circle. Recall that nosotros used values for the sine and cosine functions to calculate the tangent office. We will follow a similar procedure for the reciprocal functions, referencing the values in the unit circle for our calculations.

For example, let'due south observe the value of [latex]\sec{\left(\frac{\pi}{iii}\correct)}[/latex].

Applying [latex]\displaystyle{\sec ten = \frac{i}{\cos 10}}[/latex], we can rewrite this as:

[latex]\displaystyle{ \sec{\left(\frac{\pi}{3}\correct)}= \frac{1}{\cos{\left({\frac{\pi}{three}}\right)}} }[/latex]

From the unit circle, nosotros know that [latex]\displaystyle{\cos{\left({\frac{\pi}{3}}\right)}= \frac{ane}{2}}[/latex]. Using this, the value of [latex]\displaystyle{ \sec{\left(\frac{\pi}{3}\right)}}[/latex] can be found:

[latex]\displaystyle{ \begin{align} \sec{\left(\frac{\pi}{three}\correct)} &= \frac{1}{\frac{1}{2}} \\ &= 2 \terminate{align} }[/latex]

The other reciprocal functions tin be solved in a similar manner.

Example

Use the unit circle to calculate [latex]\sec t[/latex], [latex]\cot t[/latex], and [latex]\csc t[/latex] at the point [latex]\displaystyle{\left(-\frac{\sqrt{iii}}{2}, \frac{1}{two}\right)}[/latex].

Indicate on a unit circle: The point [latex]\displaystyle{\left(-\frac{\sqrt{3}}{2}, \frac{one}{2}\right)}[/latex], shown on a unit circumvolve.

Because we know the [latex](10, y)[/latex] coordinates of the bespeak on the unit circumvolve indicated by angle [latex]t[/latex], we can use those coordinates to find the three functions.

Recall that the [latex]x[/latex]-coordinate gives the value for the cosine function, and the [latex]y[/latex]-coordinate gives the value for the sine function. In other words:

[latex]\displaystyle{ \brainstorm{align} 10 &= \cos t \\ &= -\frac{\sqrt{3}}{ii} \end{align} }[/latex]

and

[latex]\displaystyle{ \begin{align} y &= \sin t \\ &= \frac{1}{two} \end{align} }[/latex]

Using this information, the values for the reciprocal functions at angle [latex]t[/latex] tin be calculated:

[latex]\displaystyle{ \begin{align} \sec t &= \frac{1}{\cos t} \\ &= \frac{1}{x} \\ &= \left(\frac{one}{-\frac{\sqrt{iii}}{two}} \correct)\\ &= -\frac{2}{\sqrt{iii}} \\ &= \left(-\frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{iii}} \right)\\ &= -\frac{2\sqrt{3}}{3} \end{align} }[/latex]

[latex]\displaystyle{ \brainstorm{marshal} \cot t &= \frac{\cos t}{\sin t} \\ &= \frac{x}{y} \\ &= \left(\frac{-\frac{\sqrt{3}}{2}}{\frac{i}{2}}\right) \\ &= \left(-\frac{\sqrt{three}}{2}\cdot \frac{ii}{ane} \right) \\ &= -\sqrt{three} \end{align} }[/latex]

[latex]\displaystyle{ \brainstorm{align} \csc t &= \frac{1}{\sin t} \\ & = \frac{1}{y} \\ & = \left(\frac{1}{\frac{ane}{2}}\correct) \\ & = 2 \cease{align} }[/latex]

Changed Trigonometric Functions

Each trigonometric function has an inverse function that tin can exist graphed.

Learning Objectives

Depict the characteristics of the graphs of the inverse trigonometric functions, noting their domain and range restrictions

Key Takeaways

Key Points

• The inverse function of sine is arcsine, which has a domain of [latex]\displaystyle{\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]}[/latex]. In other words, for angles in the interval [latex]\displaystyle{\left[-\frac{\pi}{2}, \frac{\pi}{2}\correct]}[/latex], if [latex]y = \sin x[/latex], so [latex]\arcsin 10 = \sin^{−ane} ten=y[/latex].
• The inverse office of cosine is arccosine, which has a domain of [latex]\left[0, \pi\right][/latex]. In other words, for angles in the interval [latex]\left[0, \pi\correct][/latex], if [latex]y = \cos x[/latex], then [latex]\arccos x = \cos^{−ane} x=y[/latex].
• The changed role of tangent is arctangent, which has a domain of [latex]\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)[/latex]. In other words, for angles in the interval [latex]\left(-\frac{\pi}{ii}, \frac{\pi}{2}\right)[/latex], if [latex]y = \tan x[/latex], so [latex]\arctan ten = \tan^{−one} x=y[/latex].

Key Terms

• inverse role: A function that does exactly the contrary of another. Annotation: [latex]f^{-i}[/latex]
• i-to-i function: A function that never maps distinct elements of its domain to the same chemical element of its range.

Introduction to Inverse Trigonometric Functions

Changed trigonometric functions are used to discover angles of a triangle if we are given the lengths of the sides. Inverse trigonometric functions can be used to determine what angle would yield a specific sine, cosine, or tangent value.

To use inverse trigonometric functions, we need to understand that an changed trigonometric function "undoes" what the original trigonometric office "does," every bit is the case with any other function and its inverse.

The inverse of sine is arcsine (denoted [latex]\arcsin[/latex]), the changed of cosine is arccosine (denoted [latex]\arccos[/latex]), and the changed of tangent is arctangent (denoted [latex]\arctan[/latex]).

Note that the domain of the inverse function is the range of the original function, and vice versa. An exponent of [latex]-1[/latex] is used to indicate an inverse function. For example, if [latex]f(x) = \sin ten[/latex],so nosotros would write [latex]f^{-1}(x) = \sin^{-1} x[/latex]. Be aware that [latex]\sin^{-i} x[/latex] does not mean [latex]\displaystyle{\frac{1}{\sin x}}[/latex]. The reciprocal function is [latex]\displaystyle{\frac{1}{\sin x}}[/latex], which is non the same as the inverse function.

For a i-to-one function, if [latex]f(a) = b[/latex], and then an inverse function would satisfy [latex]f^{-1}(b) = a[/latex]. However, the sine, cosine, and tangent functions are notone-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be i-to-one because each output in its range corresponds to at least 1 input in every period, and there are an infinite number of periods. As with other functions that are not one-to-i, nosotros volition demand to restrict the domain of each office to yield a new part that is ane-to-1. We choose a domain for each part that includes the number [latex]0[/latex].

Sine and cosine functions within restricted domains: (a) The sine function shown on a restricted domain of [latex]\left[-\frac{\pi}{2}, \frac{\pi}{ii}\right][/latex]; (b) The cosine office shown on a restricted domain of [latex]\left[0, \pi\right][/latex].

The graph of the sine office is express to a domain of [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex], and the graph of the cosine function limited is to [latex][0, \pi][/latex]. The graph of the tangent part is limited to [latex]\left(-\frac{\pi}{two}, \frac{\pi}{2}\right)[/latex].

Tangent role within a restricted domain

The tangent part shown on a restricted domain of [latex]\left(-\frac{\pi}{2}, \frac{\pi}{2}\correct)[/latex].

These choices for the restricted domains are somewhat arbitrary, only they take important, helpful characteristics. Each domain includes the origin and some positive values, and nigh importantly, each results in a one-to-i function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the side by side, instead of being divided into pieces by an asymptote.

Definitions of Changed Trigonometric Functions

Nosotros can define the changed trigonometric functions as follows. Note the domain and range of each function.

The inverse sine function [latex]y = \sin^{-one}x [/latex] ways [latex]x = \sin y[/latex]. The inverse sine part tin as well be written [latex]\arcsin x[/latex].

[latex]\displaystyle{y = \sin^{-i}x \quad \text{has domain} \quad \left[-1, ane\correct] \quad \text{and range} \quad \left[-\frac{\pi}{two}, \frac{\pi}{2}\right]}[/latex]

The inverse cosine function [latex]y = \cos^{-1}x [/latex] ways [latex]x = \cos y[/latex]. The changed cosine role can as well be written [latex]\arccos x[/latex].

[latex]\displaystyle{y = \cos^{-1}x \quad \text{has domain} \quad \left[-1, 1\correct] \quad \text{and range} \quad \left[0, \pi\correct]}[/latex]

The inverse tangent part [latex]y = \tan^{-1}x[/latex] means [latex]x = \tan y[/latex]. The inverse tangent function can also be written [latex]\arctan x[/latex].

[latex]\displaystyle{y = \tan^{-ane}x \quad \text{has domain} \quad \left(-\infty, \infty\right) \quad \text{and range} \quad \left(-\frac{\pi}{2}, \frac{\pi}{2}\correct)}[/latex]

Graphs of Inverse Trigonometric Functions

The sine function and inverse sine (or arcsine) function: The arcsine function is a reflection of the sine function about the line [latex]y = x[/latex].

To find the domain and range of inverse trigonometric functions, we switch the domain and range of the original functions.

The cosine role and inverse cosine (or arccosine) function: The arccosine part is a reflection of the cosine function most the line [latex]y = x[/latex].

Each graph of the inverse trigonometric role is a reflection of the graph of the original function about the line [latex]y = 10[/latex].

The tangent function and inverse tangent (or arctangent) function: The arctangent function is a reflection of the tangent office almost the line [latex]y = x[/latex].

Summary

In summary, nosotros can state the following relations:

• For angles in the interval [latex]\displaystyle{\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]}[/latex], if [latex]\sin y = x[/latex], and then [latex]\sin^{−1} x=y[/latex].
• For angles in the interval [latex]\displaystyle{\left[0, \pi\right]}[/latex], if [latex]\cos y = x[/latex], then [latex]\cos^{-ane} x = y[/latex].
• For angles in the interval [latex]\displaystyle{\left(-\frac{\pi}{2}, \frac{\pi}{2}\correct)}[/latex], if [latex]\tan y = 10[/latex], then [latex]\tan^{-one}x = y[/latex].

morenofouldlairity.blogspot.com

Source: https://courses.lumenlearning.com/boundless-algebra/chapter/trigonometric-functions-and-the-unit-circle/

Share this post